Versioned Iterators

Say I have iterators adhering to the following interface:

pub trait KVIter<K, V>
where
    K: Ord,
{
    fn next(&mut self) -> Option<(&K, &V)>;
    fn peek(&mut self) -> Option<(&K, &V)>;
    fn prev(&mut self) -> Option<(&K, &V)>;
    fn peek_prev(&mut self) -> Option<(&K, &V)>;
}

With the semantics that the iterator must be ordered on K, and that all K’s will be unique.

I believe the correct way to visualize such an iterator is like this:

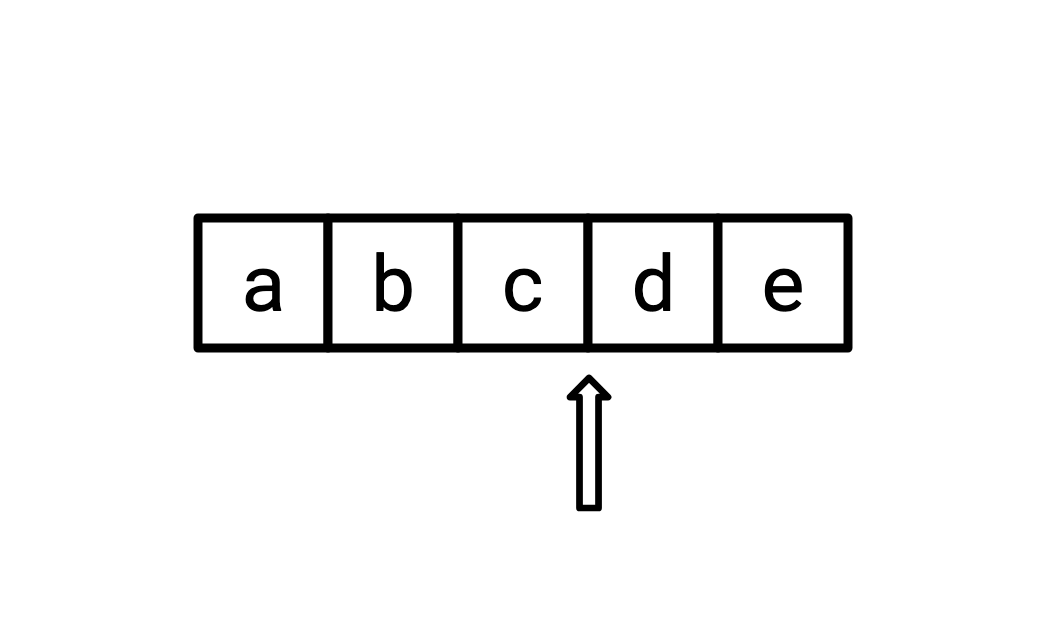
Where the current state of the iterator points to a location in-between two elements. A call to next will return d and advance the iterator one space to the right, a call to peek will return d and not move the iterator, and so on.

A thing you might often want to do in a database using MVCC is to have a dataset where some entries have the same key, but can have differing “timestamps.” We can model this by having our K in the above interface be (K, Timestamp), or just (K, usize). Log-structured merge trees like Pebble call these timestamps “sequence numbers” or “seqnums” (note that CockroachDB has a distinct layer of MVCC on top of this, which is what it refers to as “MVCC”).

Such an iterator looks the same as the above, but our keys look slightly different:

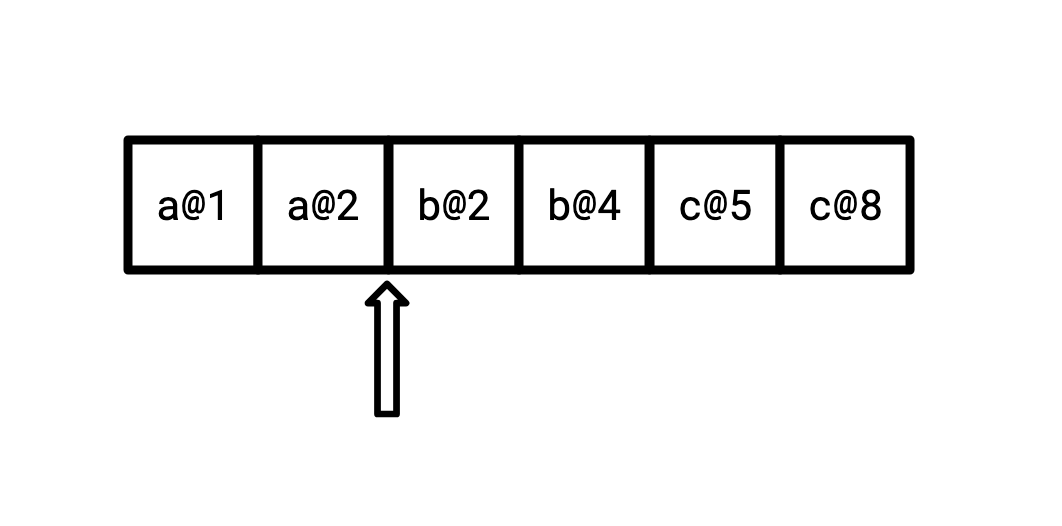
What’s more, we also want to be able to represent a value which no longer exists, that has been deleted. We can do this via tombstones, by replacing V with Option<V>, where None represents deletion.

It’s natural, then, to want to take an iterator over ((K, usize), Option<V>), plug in the timestamp t you’d like to read at, and get out an iterator over (K, V) with the values as of that timestamp. Recall the way causality works is that this means that for any key, we should observe the latest value whose timestamp is not later than t.

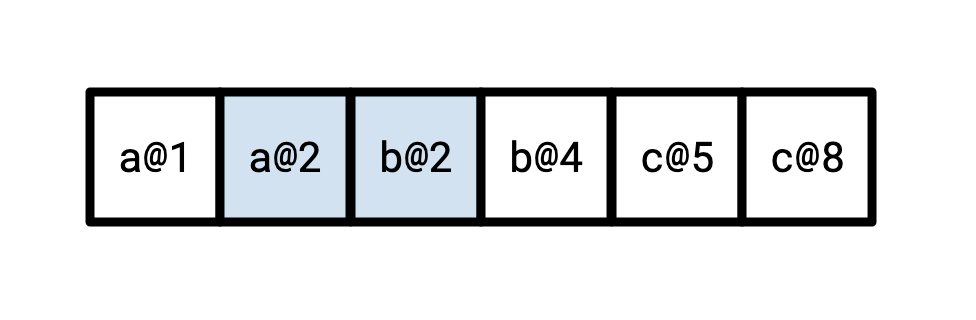
Reading at t=3 then, for instance, should yield the following coloured-in elements:

It might surprise you that writing such an iterator is actually quite tricky. It surprised me!

Why might such a thing be hard? Well, observe that first of all that there is going to be a necessary separation of logical and physical state. If we are just implementing KVIter over an underlying Vec, it’s very easy:

pub struct VecIter<K, V> {
    idx: usize,
    contents: Vec<(K, V)>,
}

impl<K, V> KVIter<K, V> for VecIter<K, V>
where
    K: Ord,
{
    fn next(&mut self) -> Option<(&K, &V)> {
        if self.idx >= self.contents.len() {
            None
        } else {
            self.idx += 1;
            let v = self.contents[self.idx - 1];
            Some((&v.0, &v.1))
        }
    }

    fn peek(&mut self) -> Option<(&K, &V)> {
        if self.idx >= self.contents.len() {
            None
        } else {
            let v = self.contents[self.idx];
            Some((&v.0, &v.1))
        }
    }

    // ...
}

And part of what makes it easy is that our logical state (where the arrow points to, in our mental model) and the physical state (idx) are always aligned. If we call peek, our logical state should not update, and, correspondingly, neither does our physical state.

Thinking about implementing what I will call SeqnumIter, this is not so: if we call peek, we will actually have to advance our underlying iterator forwards, probably several times, past all of the values sharing a key, to figure out what the next value is. Then, if we call next, we have to make sure that we return that value, and not, say, the physical next value. And so on. We could move our iterator backwards after a call to peek to re-align our logical and physical state, but a common use case for peekable iterators is to peek, and then immediately next based on the observed value, so we’re tripling our work for workloads like that.

Starting with the obvious structure of our iterator:

pub struct SeqnumIter<I, K, V>
where
    K: Ord,
    I: KVIter<(K, usize), Option<V>>,
{
    iter: I,
    seqnum: usize,
}

We’d like to support some common workloads without doing unnecessary work. Namely, a couple common, important workloads are:

• calling next over and over,
• calling peek, followed by next repeatedly, and
• calling next, then calling prev a single time, then calling next again.

We’d like to be able to handle these without constantly shuffling the underlying iterator back and forth, since doing so requires nontrivial computation. We can accomplish this with a single buffer, and by keeping track of our physical state.

pub struct SeqnumIter<I, K, V>
where
    K: Ord,
    I: KVIter<(K, usize), Option<V>>,
{
    iter: I,
    seqnum: usize,
    buf: (K, V),
    state: PhysicalState,
}

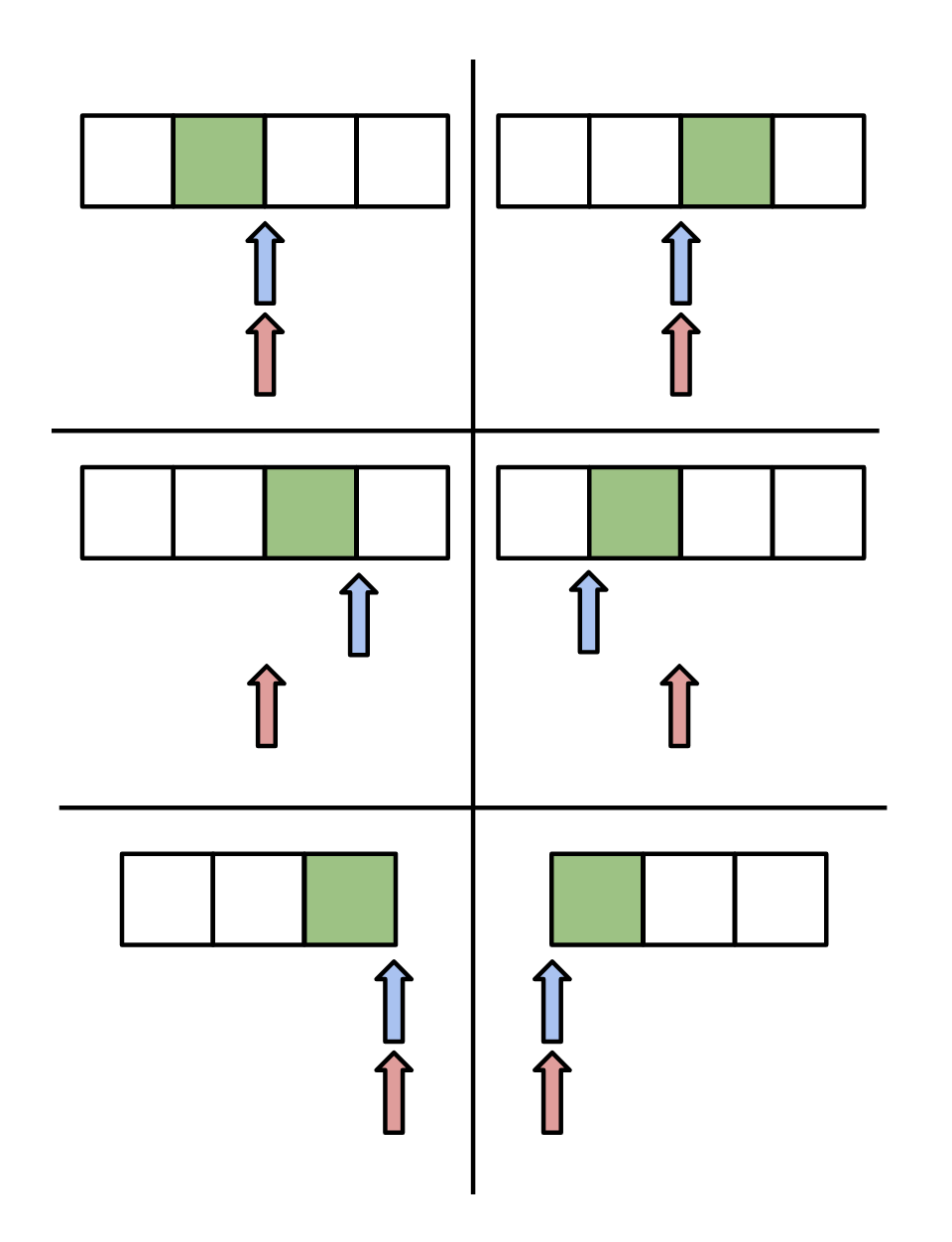
What can our physical state be? There are three dimensions:

1. Do our logical and physical locations align?
2. Does our buffer hold the value ahead or behind our logical location?
3. Are we at the start, middle, or end of our iterator?

So, logically, we imagine we get \(2 \times 2 \times 3 = 12\) possible states. It turns out many of these combinations are not actually accessible (we can’t be both at the end of the iterator and have the buffer be ahead of the logical location, for instance), and it is sufficient to have six:

enum PhysicalState {
    // Logical and physical state agree, buffer is behind logical state.
    FwdEq,
    // Logical and physical state agree, buffer is ahead of logical state.
    RevEq,
    // Logical and physical state disagree, buffer is ahead of logical state.
    FwdBehind,
    // Logical and physical state disagree, buffer is behind logical state.
    RevBehind,
    // We are at the end of our iterator.
    AtEnd,
    // We are at the start of our iterator.
    AtStart,
}

We can visualize these like this (the buffer is green, the red arrow is our logical position, the blue arrow is our physical position):

When we hand back a value to a caller, it’s always via handing a pointer to our stored buffer value, so we always need to make sure the buffer is appropriately positioned. When we move our physical position, we put the value we read into the buffer, so one way to think about it is that the buffer is populated based on which direction the physical location last traveled (forwards or backwards).

We can then write out a transition diagram for how we move between these states in response to any of our next, peek, prev, peek_prev calls. Each state transition must be accompanied by an according movement of the underlying physical iterator. Denote moving the physical operator once to the right as >, and once to the left as <. Then, if we call next, we transition as follows: 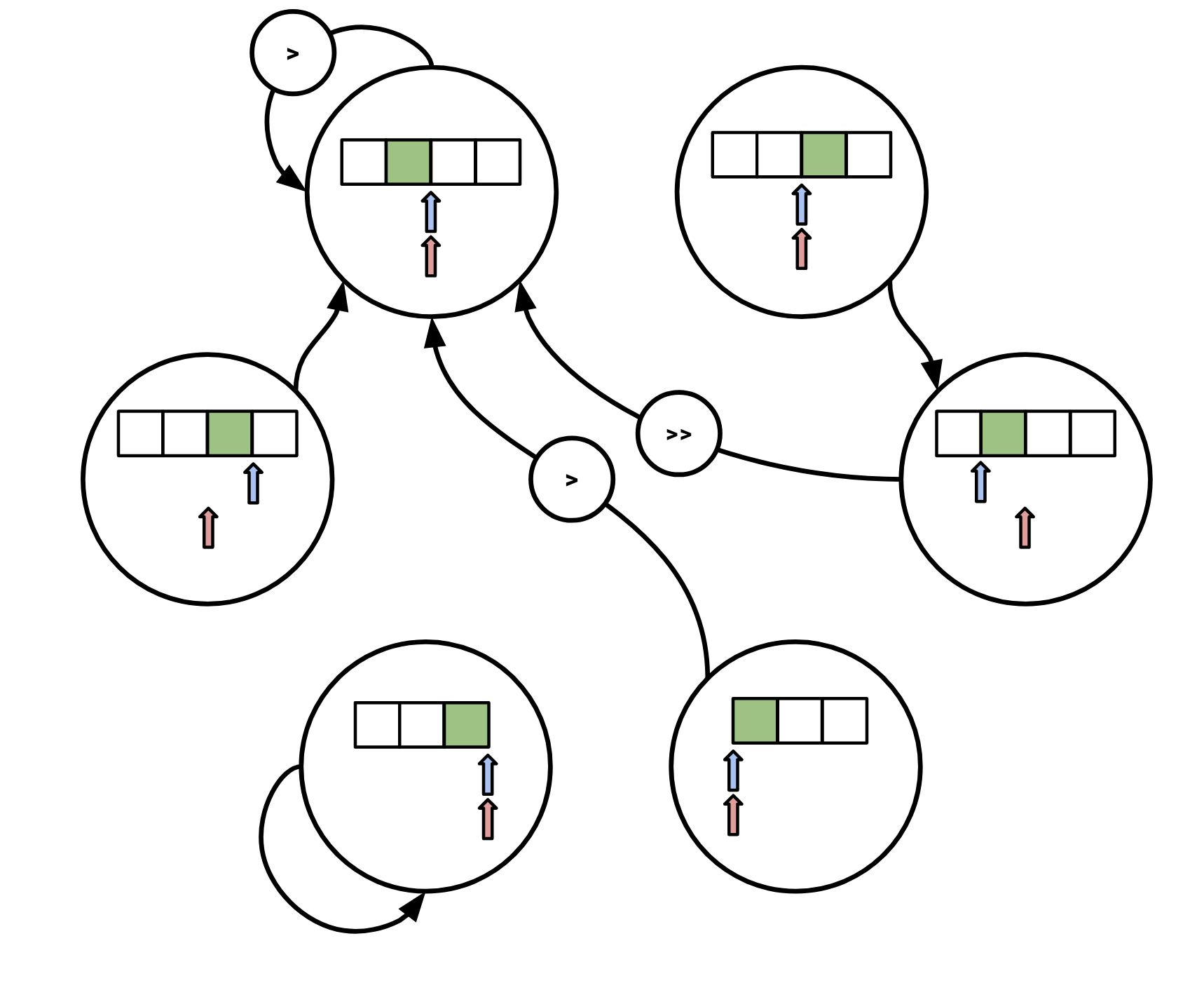Note that if we observe the end of our underlying iterator, we immediately transition to the bottom-left state (AtEnd).

The transition diagram for peek is: 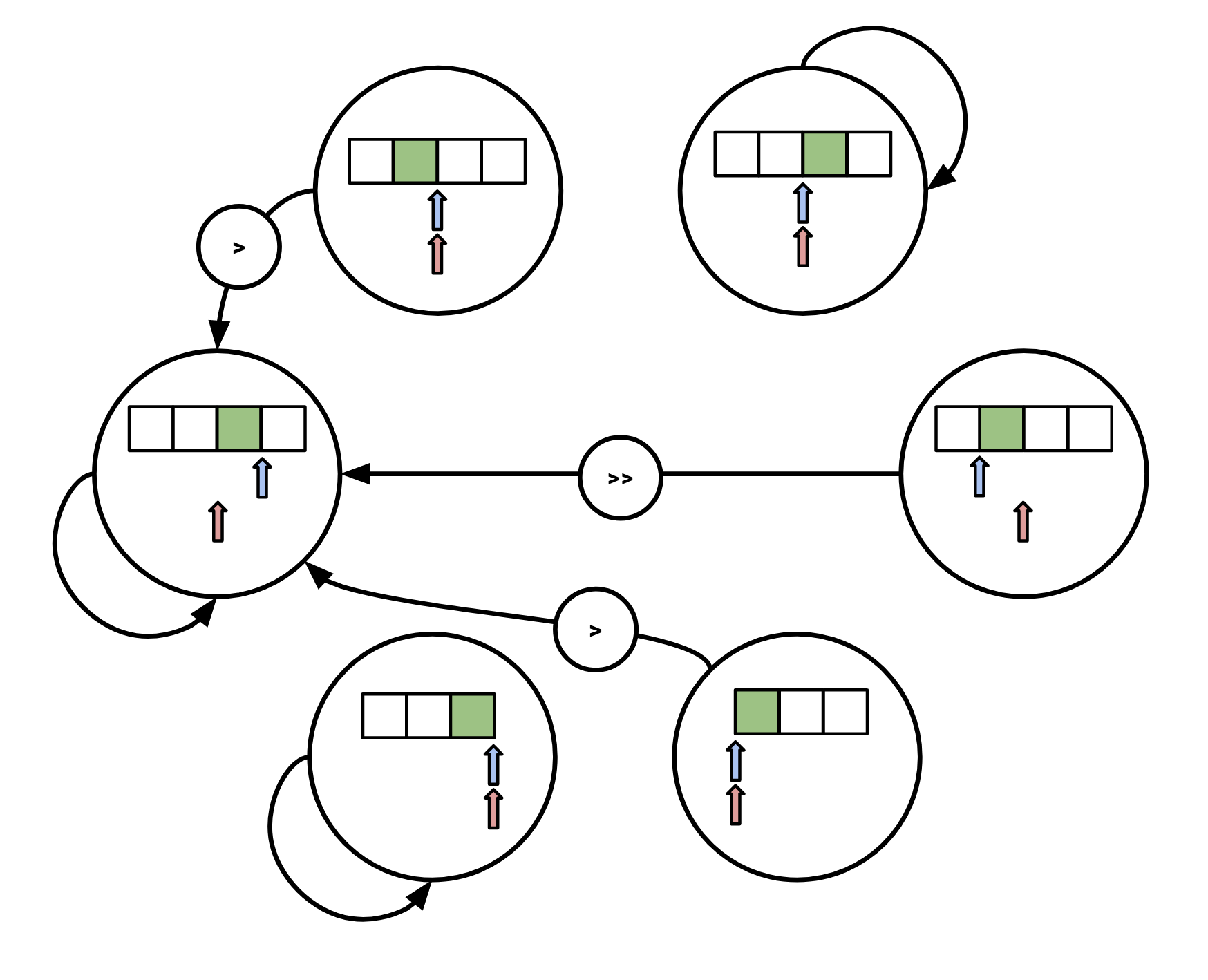Again, if we observe EOF for our underlying iterator we move to AtEnd.

The diagrams are the same but inverted for the corresponding prev methods.

These look a bit hairy, but once you have the insight of modeling this as a state machine it’s pretty easy to work out what each individual transition should be with a pencil and paper.

These then translate pretty easily into code:

fn next(&mut self) -> Option<(&K, &V)> {
    match self.state {
        PhysicalState::AtEnd => {
            return None;
        }
        PhysicalState::RevEq => {
            self.state = PhysicalState::RevBehind;
        }
        PhysicalState::RevBehind => {
            if self.physical_forwards() && self.physical_forwards() {
                self.state = PhysicalState::FwdEq;
            } else {
                self.state = PhysicalState::AtEnd;
                return None;
            }
        }
        PhysicalState::AtStart | PhysicalState::FwdEq => {
            if self.physical_forwards() {
                self.state = PhysicalState::FwdEq;
            } else {
                self.state = PhysicalState::AtEnd;
                return None;
            }
        }
        PhysicalState::FwdBehind => {
            self.state = PhysicalState::FwdEq;
        }
    };
    Some((&self.buf.0, &self.buf.1))
}

I wrote this for my own notes, and decided that it would be only marginally more effort to tidy it up into something that would be digestible by others. I was wrong, but at least I got a sharable artifact out of it.

Bilal answered many of my questions about Pebble for this post (but any misunderstandings are mine), and Ilia provided some helpful feedback.