Justin Jaffray
blog notes

Two-Phase Commit Three Ways

29 Jul 2022

To me, it’s hard to pin down what problem the two-phase commit (2PC) protocol solves.

Usually, the stated goal is “atomic commitment,” which, without further elaboration, FLP impossibility and the Two Generals Problem tell us can’t be done in general. So what’s the deal? What is this thing for?

I think the fact that this question doesn’t have an immediately satisfying answer is unsurprising; 2PC is such a natural, simple algorithm that you really shouldn’t expect it to look tailor-made to a problem. After all, the entire protocol is:

Talk to everyone, then talk to everyone again.

For this reason, I think the best way to understand 2PC, and by extension, other atomic commitment protocols, comes from looking at it from a few different perspectives.

We’re going to approach this from first principles as someone who knows nothing about 2PC, and start with a few motivating problems that will lead us to a solution.

1. Evaluating a Particular Expression

The first perspective we’ll see is to evaluate the expression \[ x_1 \wedge \ldots \wedge x_n. \] That is, there’s a number of boolean variables and we want to compute their “and,” or “conjunction.” There are two catches though:

  1. we don’t know the values of all the variables. Our friends, named \(c_1\) through \(c_n\), each know the value of the corresponding \(x_i\).
  2. our friends also want to know the value of our big conjunction.

The most natural approach to this situation directly gives something resembling 2PC.

  1. ask everyone for their \(x_i\),
  2. compute \(x = x_1 \wedge \ldots \wedge x_n\),
  3. tell everyone the value of \(x\).

This models the situation where every participant has a “vote,” or an opinion on whether a “commit” should take place, and we merely want to find out the answer and broadcast it.

Another way of thinking about this interpretation is that we want to know when our conjunction becomes true. The initial question to friend \(c_i\) “tell me the value of \(x_i\)” could also be “let me know when \(x_i\) becomes true.” This interpretation makes sense assuming that \(x_i\) is the sort of information that starts out false, possibly becomes true, then never becomes false again, such as “did you complete that piece of work I assigned you?”

So there’s our first perspective: we want to compute a big conjunction, so we do the most obvious possible thing. There is more to it than this, however. Which we will see in our second presentation.

2. Barriering a State Machine

The second perspective we’ll discuss is that of commitment.

The setup now is not that our friends have some secret piece of knowledge, but that they can be modeled by a state machine. This state machine has two important states: not yet and yes. When we ask someone to, they will change their current internal state.

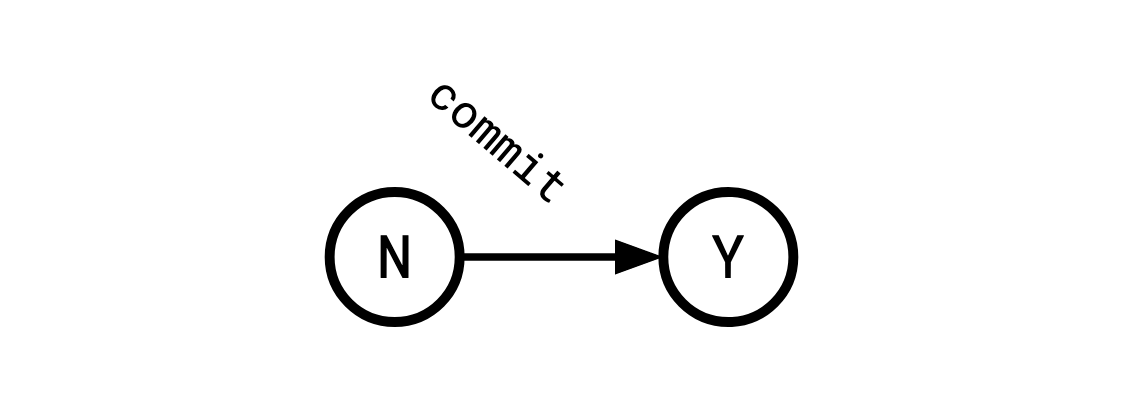
We’d like to move everyone from not yet to yes, but a constraint we have is that it shouldn’t be the case that someone is in not yet at the same time someone else is in yes. If this constraint feels unmotivated, think of it as “nobody should be in yes while someone else isn’t even aware we’ve begun this process.”

Given this, the following algorithm has obvious deficiencies:

This doesn’t meet our requirement at all in the event of nonzero network delays: if I merely send my messages sequentially I’ll have some people in not yet and some in yes. Not to mention what happens if we, the coordinator, fail, in which case we might have an extended period of time where some people are in not yet and some are in yes.

The most natural solution to this problem is to simply introduce an intermediate state, named unsure:

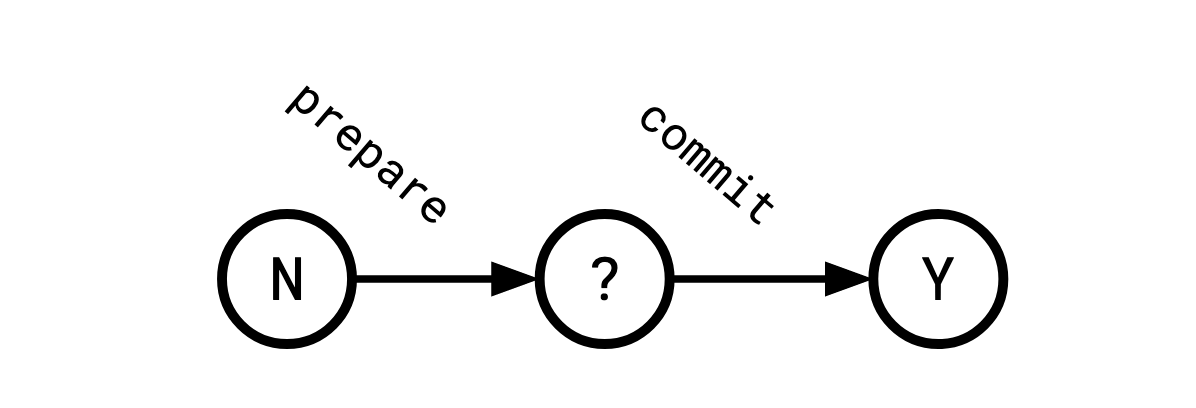
Which implies a different protocol:

  1. Tell everyone to move to unsure (prepare).
  2. Wait for them all to acknowledge my message.
  3. Tell everyone to move to yes (commit).

Which is again 2PC. Now only the following combinations of states are possible:

  1. everyone in not yet,
  2. some people in not yet, some in unsure,
  3. everyone in unsure,
  4. some people in unsure, some in yes,
  5. everyone in yes.

I like to visualize this as a sliding window of the possible extant states:

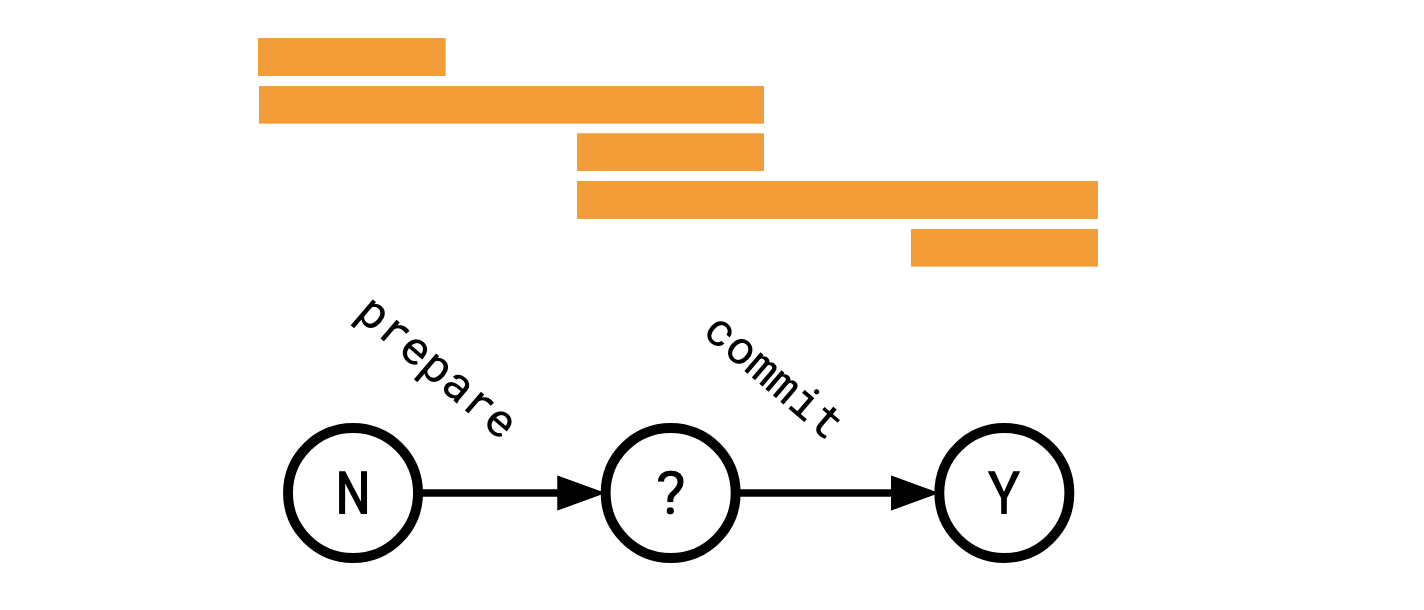
Importantly what this does is give a level of local reasoning to the participants, if a participant loses contact with the coordinator:

And in fact this can be extended to an \(n\)-phase commit algorithm with the same constant-size sliding window.

But it’s still not really clear what this accomplishes. And for this we need to combine these two ways of thinking about 2PC.

3. The Synthesis

Taking both of the previous perspectives and considering them at once yields a third, more complete perspective.

In this setting, everyone has a secret boolean value and a state machine. The boolean is now the answer to “I would like to move you to yes, are you okay with that?” And again, everyone wants to know the value of said conjunction, which, in this case, has the interpretation “is everyone okay with being moved to yes?”

Once they’ve been asked this question, they’ll move to unsure. If, indeed, everyone is okay with it, they will all step forward and move to yes. If anyone objects, everyone aborts.

The complete protocol is thus:

Under this melded perspective, our state machine looks like this, where we enhance the perspective two state machine with “actually, we decided not to do this”:

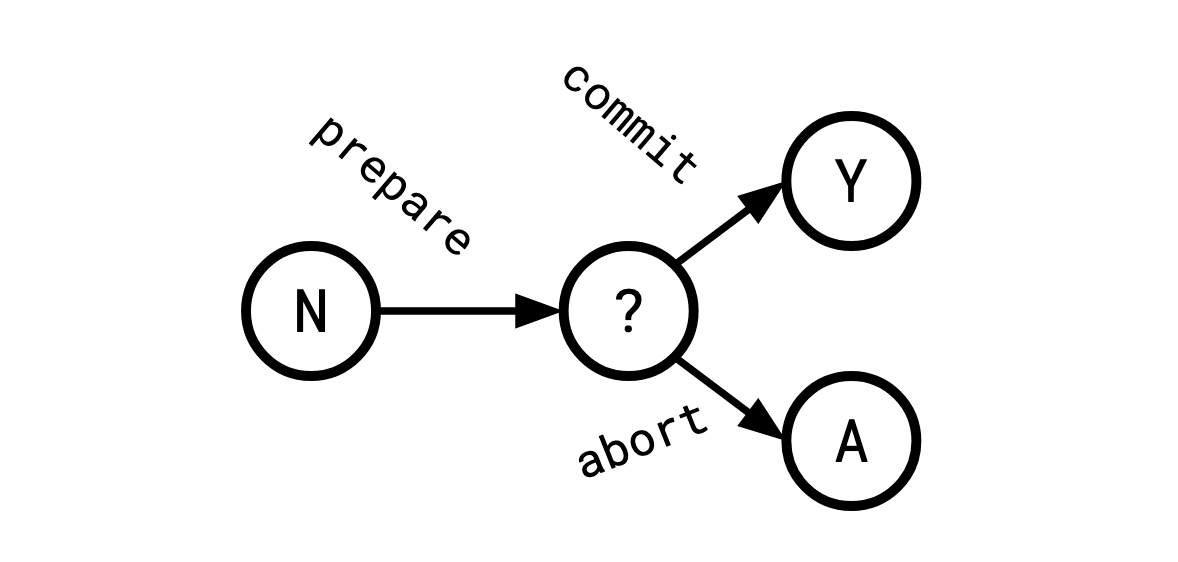
Notice that when a participates responds “yes” in the first phase, they are in fact promising “should you tell me to, I will move to Y.” This means that if their response of “yes” was conditional upon some internal state they hold (nobody else holds a lock on the piece of data moving to Y requires modifying, for example), they are now obligated to protect that state of the world with their own lock.

For the duration of time where a participant is in ?, they must ensure that they remain able to move to Y or A.

This is the crux of this melding, and why I think this is a useful way to present this idea: sending a PREPARE message to someone does not one, but two things:

  1. tells you that they are on-board to commit, in the future,
  2. obliges them to continue to be on-board to commit.

This is a bit abstract, so let’s see a concrete example. Say you’re trying to organize a get-together with a group of friends on Saturday. One way this might go is to talk to each of them in turn:

The analogy is a little tortured, but imagine if instead of irreversibly committing to attending on Saturday, our friends were some third-party service that we didn’t have the ability to reverse a decision on.

Using 2PC, this would look like this:

Here’s the point: from here, it looks like 2PC is actually just locking: PREPARE takes a lock on the ability to do something, and COMMIT simultaneously acts on the data and releases the lock (writing a 2PC explainer, I’m legally obligated to remark that 2PC is distinct from two-phase locking, a different algorithm1).

One could even generalize these locks a bit, to not be merely on the resource that the commit will operate on:

Conclusion

I personally find 2PC quite subtle. I think there are two primary reasons for this.

  1. The algorithm itself is very very simple, and as a result, doesn’t really imply what the various parts of it are for or what exactly it’s tolerating.
  2. 2PC ostensibly exists for some level of fault-tolerance, but you would use it even in the absence of the possibility of faults, because it’s actually about locks. Recovery is a component of the algorithm but the model can vary a lot and is not typically made explicit.

Even if you don’t have these same concerns, I hope this discussion was helpful.

Footnotes

  1. Not as different, I think, as all of those prominent warnings imply.