Deduplicating Decklists

17 Sep 2020

This is not going to be my normal kind of post, it’s not very focused, and going to be a bit rambley, as I talk about a problem I thought about one day.

Magic: The Gathering is a card game where players construct decks, typically of 60 cards plus a 15 card sideboard, for 75 cards total.

Periodically, the company that makes the game, Wizards of the Coast (WotC) publishes a list of decks that did well recently. Just recently they announced that they were going to start doing this for their most recent digital offering of the game. Stay with me! This isn’t a post about card games. This list, however, is doctored: they want the data shown to be broad and not repetitive, so they perform some amount of deduplication on the data. This means that if two “similar” decks do well, only one will be shown in the dump. The linked article outlines what is meant by “similar:”

We will be publishing lists from Standard Ranked, Traditional Standard Ranked, Historic Ranked, and Traditional Historic Ranked play queues. Like we do for Magic Online Leagues, we will be posting an example list for each category of deck that share a minimum number of cards: at least 55 of 75 cards (across main deck and sideboard) shared in Traditional (best of three games, or Bo3) or at least 45 of 60 main deck cards shared in best of one (Bo1). All lists published will have won at least six consecutive matches.

This seemed to me like an interesting problem! Given a raw set of decks that did well, how could we produce such a deduplicated set of decks?

At a high level, we might envision the set of decks as a bunch of points in some space, where points are closer together if the decks are more “similar” (for some meaning of “similar” we haven’t made precise yet).

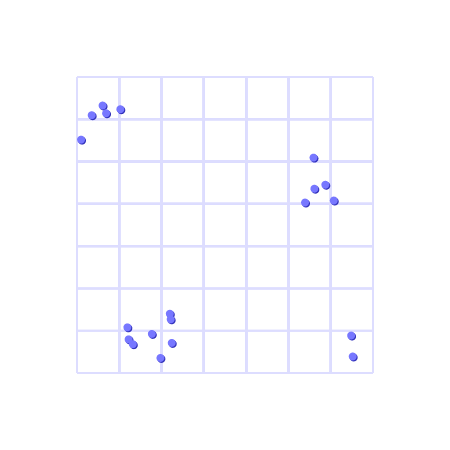
With a solution being a set of decks which “cover” the set of all other decks (for some meaning of “cover” we haven’t made precise yet).

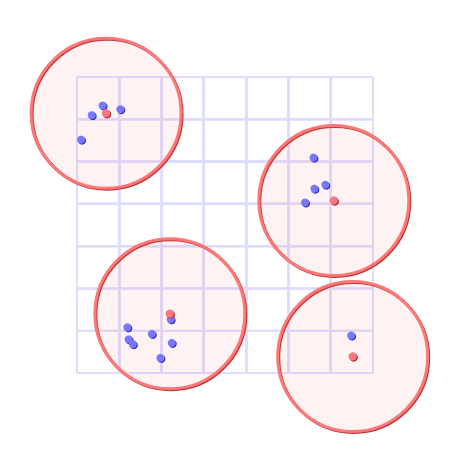
To be slightly more precise, given a set \(D\) of “decks,” we want to find a minimal set \(D^\prime \subseteq D\) such that every \(d \in D\) is “sufficiently close” to some \(d^\prime \in D^\prime\).

Let’s define what we mean by “deck” and “sufficiently close.” We can represent decks as maps from the set of cards \(C\) to some integer \(n \in \mathbb N\) denoting how many copies of a given card are in the deck. We might also think of this as an \(\mathbb N\) vector indexed by \(C\), which can be denoted \(\mathbb N ^ C\). That’s all to say, you should think of one of these decks as just a sequence of numbers denoting how many of a given card were included, where each index corresponds to a particular card: \[ \langle \ldots, 4 \ldots, 2, \ldots, 1, \ldots, 4, \ldots \rangle \] The sequence is finite, since there’s a finite number of Magic cards (about twenty thousand).

For “closeness” of two decks, per the statement above from WotC we are interested in the total number of different cards between them. That is, the distance between two decks \(a\) and \(b\) is the sum of the absolute difference of the quantity of each card: \[ |a - b| = \sum_{c \in C} \left| a_c - b_c \right|. \] This way of measuring distance is pretty natural, and satisfies some nice properties:

1. \(|a - b| = 0\) if and only if \(a = b\),
2. \(|a - b| = |b - a|\) (symmetry), and
3. \(|a - c| \le |a - b| + |b - c|\) (triangle inequality).

A notion of distance that satisfies properties 1, 2, and 3 happens to be called a metric, and a set combined with a metric on that set is called a metric space. This particular metric we’ve stumbled on is actually well known, and is called the \(\ell_1\)-norm.

We’ll be a little abstract here, but when you hear “metric” you should just think “way of thinking about distance.” If you look at the three properties, they’re all pretty natural things you’d want from a measure of “distance:”

1. says the only thing “zero distant” from a thing is the thing itself,
2. says that \(a\) is exactly as far from \(b\) as \(b\) is from \(a\), and
3. says two things can’t be further away than the sum of their distances to a third thing.

There are lots of metrics people use for various things. Another one is the \(\ell_2\)-norm, which you might also know as Euclidean distance: if you have two points in Euclidean space and draw a straight line between them, their \(\ell_2\)-distance is the length of that line. In two-dimensional space, \[ |a - b| = \sqrt{(a_x - b_x)^2 + (a_y - b_y)^2} \] Which is just the Pythagorean theorem. For our problem we’re concerned with the \(\ell_1\)-distance, as described above.

Why bother introducting this abstraction? Well, mostly I just thought it was kind of neat, but I think making this kind of hop upwards the abstraction hierarchy can be useful to understand problems sometimes, because it lets us make concrete the link between our actual problem, \(\ell_1\)-distance of 20,000-dimensional \(\mathbb N\)-points, weird, scary, hard to visualize, to a problem which is easier to conceptualize: \(\ell_2\)-distance of two-dimensional points.

Seen this way, this kind of picture isn’t just a helpful mental model, but it actually has a real, quantifiable link to the original problem we were trying to solve.

When thinking about this problem, it’s not completely accurate, but it’s not too bad to just imagine the \(\ell_2\) picture above.

Remember that the thing we’re primarily interested in is going to be all the points “sufficiently close” to a given point, where “sufficiently close” means “has distance less than some \(r\).” It turns out this thing has a name, the (closed) ball of radius \(r\) centered at \(p\) is the set of points \(x\) satisfying \(|x - p| \le r\). A “ball” is basically what you expect in most contexts, in 2D space, under the \(\ell_2\)-norm (our diagram above) a ball is a (filled in) circle. In 3D it’s a sphere. In “deck-space,” it’s the set of decks you can make from \(p\) by adding and removing at most \(r\) cards.

This lets us rephrase our problem a bit more generally. Given a metric space \(M\), a finite set of points \(P \subseteq M\), and a radius \(r\), we want to find a set \(P^\prime \subseteq P\) such that every \(p \in P\) is within some ball of radius \(r\) centered at some \(p^\prime \in P^\prime\).

So, can we solve this problem, in a general metric space, efficiently? It turns out we actually can’t! Why did I bother going down this road of generalization if it was going to lead to a dead-end? Well, it’s the road I took when thinking about this problem and it’s my blog, and also it’s actually easy to show that the problem at this level of generality is NP-hard. As a reminder, to show this is NP-hard for metric spaces in general, we must:

1. Fix some metric space, and
2. show that computing the size of the cover is NP-hard by showing that an efficient solution to that would allow us to solve some other NP-hard problem.

Consider a graph \(G\):

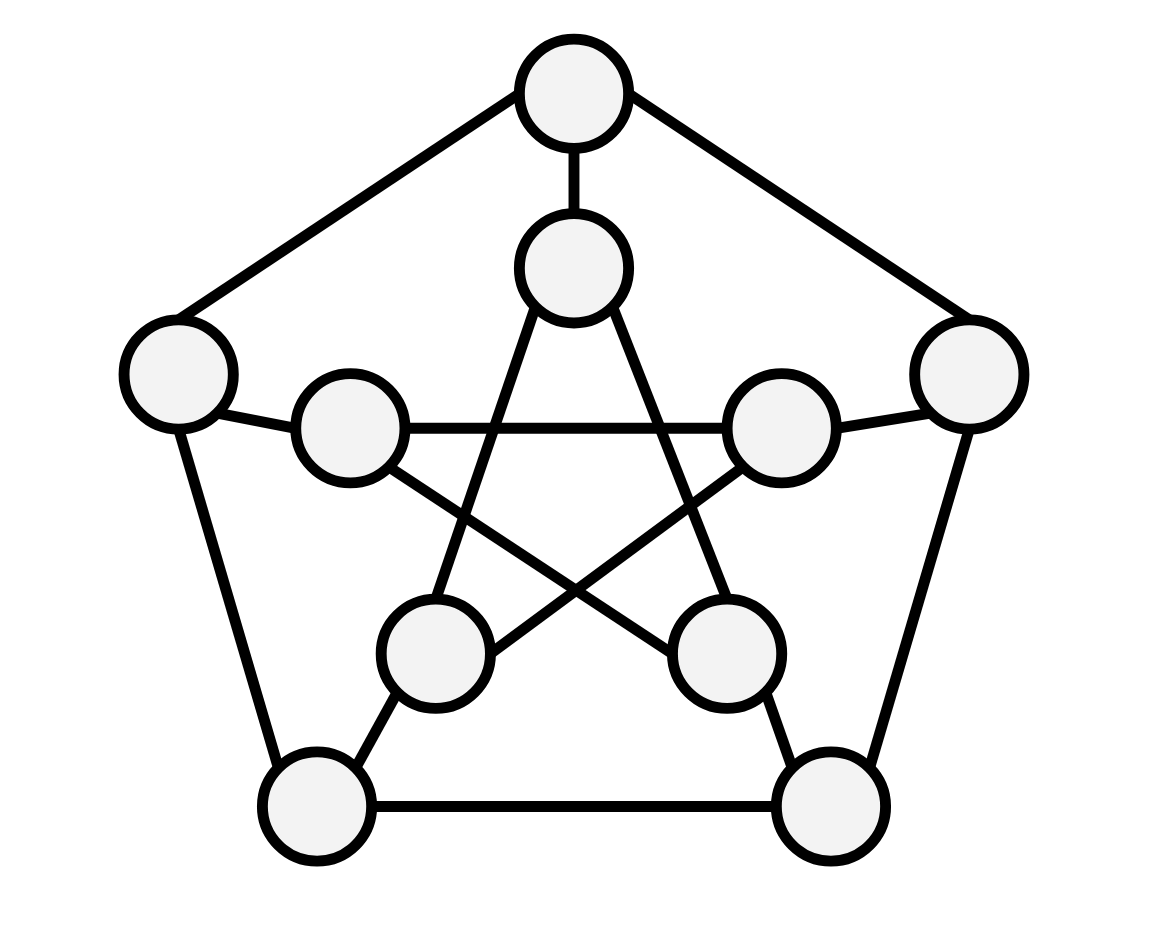
The dominating set problem is this: given a graph \(G = (V, E)\), find a set \(V^\prime\) of vertices such that every \(v \in V\) is adjacent to some \(v^\prime \in V^\prime\). That is, we want to choose some set of vertices that “cover” all other vertices: every other vertex is adjacent to one we chose. Finding a minimum dominating set is a well known NP-complete problem, and already smells similar to our problem!

If we define a binary function on the vertices of \(G\): \[ d(a, b) = \text{the length of the shortest path between $a$ and $b$}, \] it turns out \(d\) is a metric (check this yourself, it’s easy)!

If we take this metric and set \(r\) to 1, we’ve exactly recreated the dominating set problem, which, being NP-complete, means our problem in a general metric space is also NP-complete. While this doesn’t mean that our original problem about Magic decks is NP-complete (though it’s evidence that suggests this might be the case), it does mean that any algorithm that only uses the properties of a metric space probably doesn’t have an efficient solution.

When asked about this, my friend Forte found a nice reduction from 3SAT to the deck problem if \(r\) is at least four. The gist of it is this:

• Given an instance of 3SAT with \(n\) variables \(\{v_1, \ldots, v_n\}\), let your set of “cards” be \(\{x_1, \ldots, x_n\} \cup \{y_1, \ldots, y_n\}\).
• For each clause \(a \vee b \vee c\), take the vector that is 1 at \(x_i\) for the variable for \(a\) if \(a\) is not negated, and -1 if it is, and the same for \(b\) and \(c\).
• For each variable \(v_i\), add three vectors that are all 2 at \(y_i\), and -1, 0, and 1 at \(x_i\), respectively (the choice of the one at 1 or -1 will correspond to whether we take that variable to be true or not, and the 0 one is there to ensure you need to take at least one of them).
• This set of decks has a cover of size \(n\) (for radius 4) if and only if the 3SAT instance was satisfiable (the numbers can be tweaked to support radii larger than 4).

If \(r\) is one then there actually is an efficient solution, because in this case the adjacency graph is bipartite, and a dominating set of a bipartite graph can be found in polynomial time. I don’t know if there’s an efficient solution when \(r\) is two or three.

Ok, well, we are probably not going to find an efficient solution then, how about an inefficient solution? Wizard of the Coast must have some way of doing that, since they regularly publish such deduplicated decklists. The likely answer, I’d guess, is that they don’t fret about finding the minimum cover, and just do something like “output uncovered decks until none remain.” Or possibly there are just few enough decklists that they have an excel spreadsheet or something that makes sure their stated invariants are upheld. Unsure! If you work at WotC and somehow came across this post I’d be curious to learn the real answer.

I can’t say how they actually do it, but there are plenty of heuristic methods for solving this kind of thing that they might employ if you’re actually interested in finding a good solution.

Techniques like Branch and Bound or simulated annealing are good general purpose strategies for this kind of problem. I will once again shill for In Pursuit of the Traveling Salesman if you’re interested in a (somewhat) light read on how to think about this kind of thing!

Since in branch ‘n’ bound we need to be able to lower bound an instance of the problem, I will leave you with a fun lower-bounding strategy for instances of this problem: a set of \(n\) points all pairwise \(2r\) away from each other lower-bounds a solution to at most \(n\) points, since no two of those points can be covered by the same ball. There might be more, and better ones, but this was the nicest one I could think of!

This post would not exist without very helpful discussion from my math advisory Ilia and Forte and my Magic: the Gathering advisory Julian.